Fundamental counting principle
Refer back to the Learning Activities titled “A Formula for Permutations” and “A Formula for Combinations.” Explain how the Fundamental Counting Principle is used each time the Permutation Formula (nPr) or the Combination Formula (nCr) is applied. Would these be considered independent or dependent events? Or, is it inappropriate to be concerned about whether it is independent/dependent? Explain your thinking on the question.
A Formula for Permutations
Introduction
Formulas can be a very efficient way of solving problems. For the permutation formula introduced in this section, identify all the relevant variables. How does the formula function? How does it align to other methods of solving permutation problems?
Max needs to figure out how many possible route options he has going from one city to another on his two-week vacation in Europe. He has 10 cities on his itinerary and would like to visit at least three of them. How many possible route options does Max have, if he goes to three of the 10 cities during his vacation?
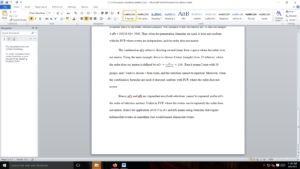
Now suppose there are 10 locations and only three stops can be made over a given time period. In this case, how many ordered three-stop routes out of 10 possible stops can be considered? We could use the method:
, or we can use the permutation rule where k items are to be selected from n available items. When order matters, this idea is notated where
nPk=n!(n−k)!
To solve this particular routing problem, use n = 10 and k = 3.
That is, out of 10 locations, there are 720 possible three-location routes.
| Note: A permutation function is included on most modern scientific calculators. You may find it in the menu of functions under “probability.” |
|---|
Moreover, you can see that this does conform to the fundamental counting principle. There are 10 locations to choose from for the first stop, then nine for the second, and eight for the third.
Try This!
A company employs 24 engineers, and an event requires four 15-minute presentations given by engineers. How many different lineups for presentations are possible?
(c) Thinkstock
Solution: Here we need to select four engineers out of 24, where order is relevant. Therefore, we will use the permutation rule,
Answer: 255,024 lineups
Permutations
The following video tutorial explains how to evaluate factorials, use permutations to solve problems, and determine the number of permutations with indistinguishable items.
(Mathispower4u, 2010)
Requirements: More than 15 characters, less than 4000 characters
Answer preview
The combination nCr refers to choosing several items from a space where the order does not matter. Using the same example above to choose 4 items (sample) from 10 (objects) where the order does not matter is defined by . Here it means I start with 10 people, and I want to choose 4 from them, and the selection cannot be repeated. Moreover, when the combination formulae are used, it does not conform with FCP, where the order does not matter.
Hence, nCr and nPr are dependent since both selections cannot be repeated, and in nCr, the order of selection matters. Unlike in FCP, where the events can be repeated, the order does not matter. Hence the application of FCP in nCr and nPr means using formulae that require independent events on something that would require dependent events.
[310 Words]
Fundamental counting principle

